Euklidovské transformácie sú vhodné na menenie polohy v priestore, zachovávajú veľkosť útvaru. Matica lineárnej transformácie má tvar:
(x, y, z, 1) ® (x´, y´, z´, 1)
x´ = f (x, y, z),
y´ = g (x, y, z),
z´ = h (x, y, z)
A´ = A .T
Identita, základný stav:
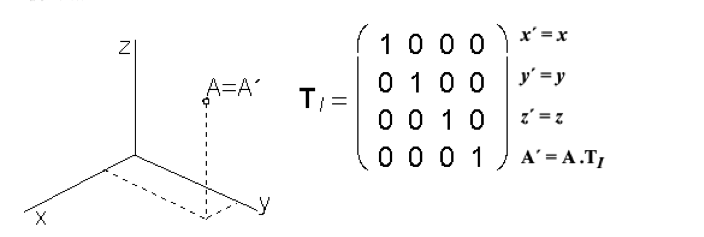
Základné transformácie:
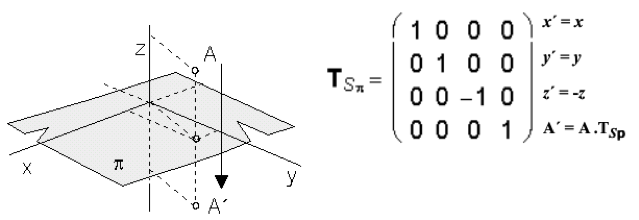
Rovinná súmernosť podľa súradnicovej roviny p = xy:
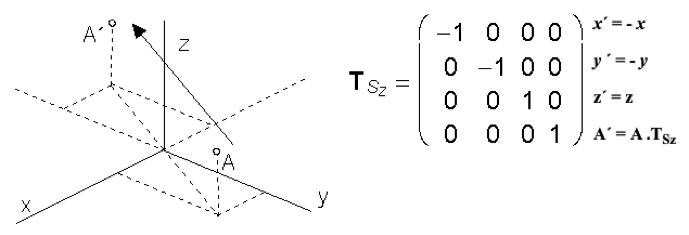
Osová súmernosť podľa súradnicovej osi z:
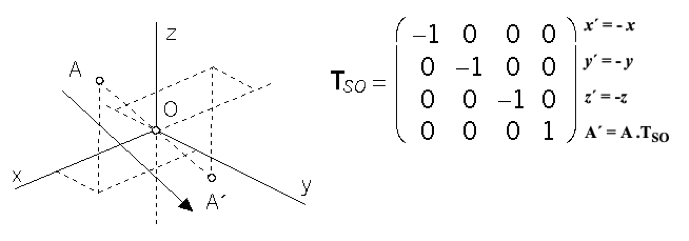
Stredová súmernosť podľa začiatku súradnicovej sústavy O:
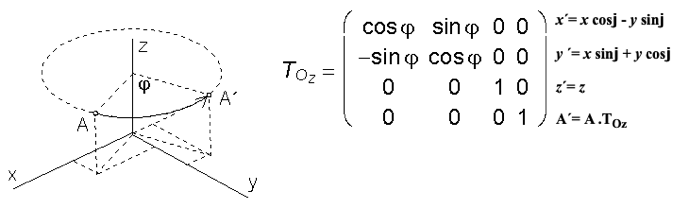
Otáčanie okolo osi z o uhol j:
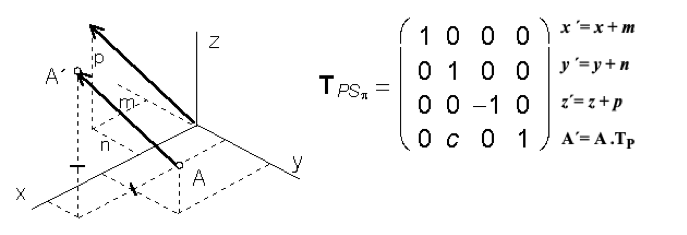
Posunutie o vektor (m, n, p, 0):
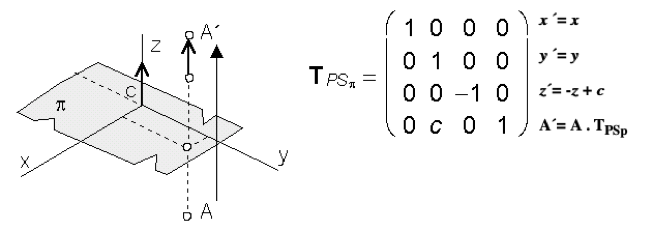
Posunutá rovinová súmernosť podľa súradnicovej roviny p s posunutím o vektor (0, c, 0, 0):
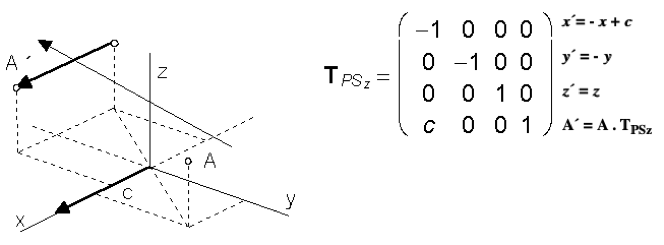
Otočená rovinová súmernosť podľa súradnicovej roviny mokolo súradnicovej osi x:
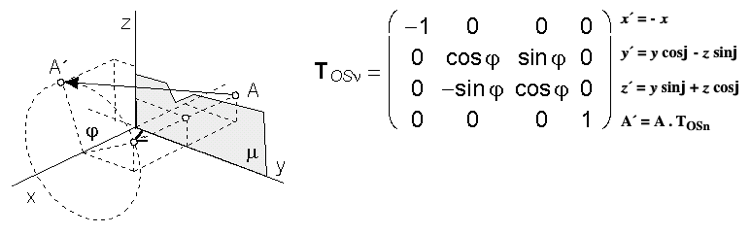
Skrutkový pohyb okolo osi zs posunutím o vektor (0,0,v,0) pre uhol otočenia j:
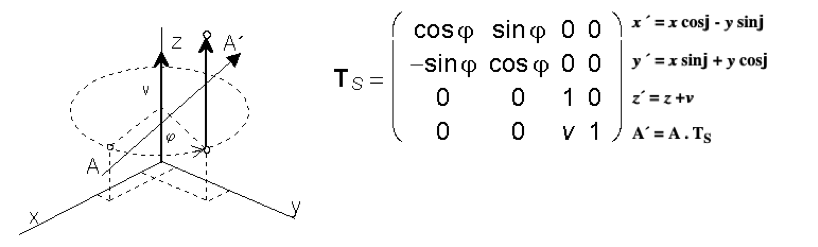
Afinné transformácie
Afinné transformácie nezachovávajú veľkosti úsečiek a uhlov. Každá euklidovská transformácia je afinnou transformáciou (podobnosťou) v .
Všeobecná afinná transformácia:
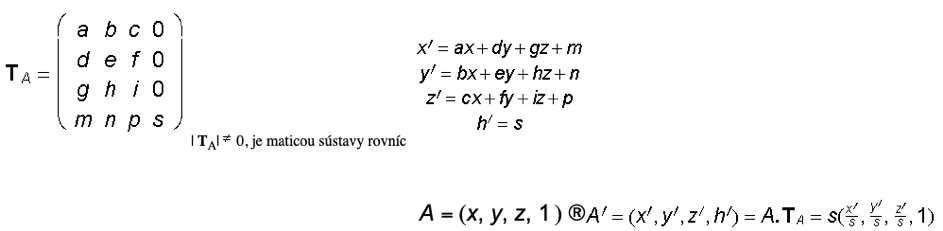
Rovnoľahlosť s daným stredom O a nenulovým koeficientom rovnoľahlosti s (zmena mierky):
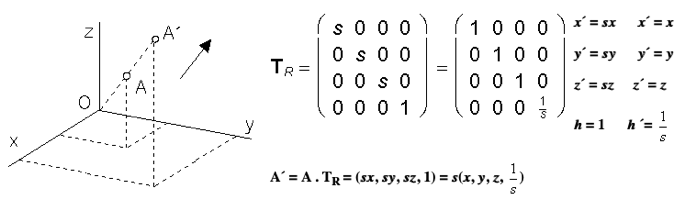
Osová afinita medzi rovinou p = xy a rovinou p´ = xA´ s osou v osi x a odpovedajúcou si dvojicou bodov A(a, b, 0, 1) ® A'(d, e, f, 1), b 0, f 0, so smerom afinity určeným priamkou s = AA' so smerovým vektorom
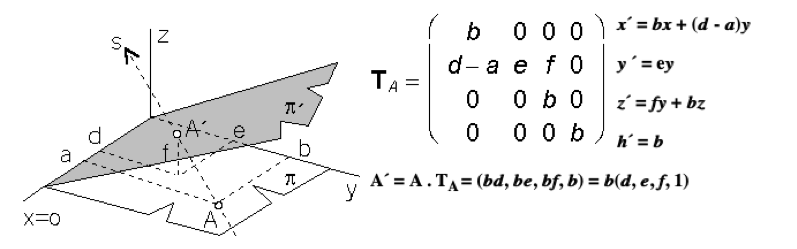
Zdrojový kód: