Sférické súradnice a vektory

V prípade simulovaného robotického futbalu sa používajú tzv. Sférické súradnice. Je to system súradníc, ktorý sa skladá z troch komponentov:

• r – vzdialenosť
• θ – vertikálny uhol (medzi Z a Y)
• φ – horizontálny uhol (medzi X a Y)

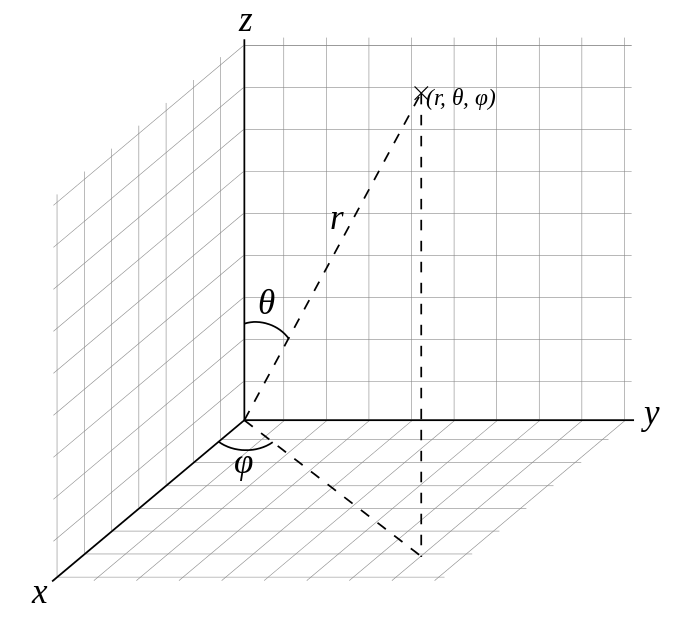
Obr. 1: Ilustrácia sveta pomocou sférických súradníc

Ako možno vidieť na Obr. 1: Ilustrácia sveta pomocou sférických súradníc, horizontálny uhol označuje o koľko stupňov sa objekt predomnou nachádza vľavo/vpravo (0 = priamo predo mnou) a vertikálny uhol určuje pod akým uhlom je objekt k mojmu perceptoru naklonený (POZOR ! je to uhol pri objekte nie pri perceptore – hlave) Dĺžka úsečky od perceptoru k objektu je označená ako r – vzdialenosť. Jednotlivé delty potom označujú posun objektu voči agentovi v rámci jednotlivých osí.

Správy zo servera o objektoch (hráči, lopta a fixné body) prichádzajú do agenta v sférických súradniciach. Pre prevody sférických súradníc na kartéziánské a naopak slúži trieda Vector3D. Na základe týchto prevodov je možné vypočítať relatívne súradnice objektov pre systém so začiatkom na mieste agenta.

private static Vector3D spherical(double r, double phi, double theta) {
   Vector3D vector = new Vector3D();
   vector.r = r;
   vector.phi = phi;
   vector.theta = theta;
   vector.theta_deg = toDegrees(theta);
   vector.phi_deg = toDegrees(phi);
   vector.calculateCartesian();
   return vector;
}

Kod 1: Prevod do karteziánskych súradníc

private static Vector3D getPolarCoordinates(SArray message) {
  SObject object = message.getOnIndex(0);
  if(object != null && object instanceof SString) {
     if (((SString) object).getString().equals("pol")) {
        // ...
        return Vector3D.spherical(r, toRadians(phi), toRadians(theat));
     }
  }
  return null;
}

Kod 2.: Prevod na sférické súradnice

Trieda Vector3D zároveň implementuje operácie spojené s vektormi, ako aj možnosť vytvorenia nového vektora na základe kartezianských alebo sférických súradníc. Pre zvolenú možnosť je následne vykonaný prepočet do druhej sústavy a je vrátený vektor obsahujúci komponenty pre obe sústavy.