Algoritmus, ktorý používa sériu meraní pozorovaných v priebehu času, obsahujúcich štatistický šum a iné nepresnosti na odhad premenných v širokom spektre procesov. Využíva k tomu nielen naposledy nameraných dát a model systému, ale aj vektor údajov o predchádzajúcom stave systému. Je široko používaný pre spracovanie signálov, navigáciu, robotiku a ďalšie úlohy.

Kalmanov filter hľadá optimálny faktor zmeny pre nasledujúci stav meranej veličiny. Vychádza z predpokladu, že nevieme presne veličinu zmerať ani odhadnúť so 100% istotou. Predpoklad je mať buď linearizovaný model správania, alebo v pokročilej verzii algoritmu sa meraný model linearizuje. Do úvahy sa berú tiež predchádzajúce stavy a ich odhady.

• Jednoduché formulovanie a implementácia s ohľadom na základné pochopenie
• Meracie rovnice nemusia byť obrátené
• Dobré výsledky v praxi z dôvodu optimality a štruktúry
• Pohodlná forma pre online spracovanie v reálnom čase

VuvedenýchrovniciachA ,B aH sú matice,k ječasovýindex,x je tzv. stav systému,u je známy vstup do systému aw az sú šumy.Premennáw reprezentuje tzv. procesný šum az tzv. merací šum.Každáztýchtoveličínje (obvykle) vektor a preto obsahuje viac akojednuzložku.Vektorx obsahuje všetkydostupnéinformácieosúčasnomstavesystému, ale niejemožnéhomeraťpriamo.Namiestotohomeriamey , ktoré je funkciou x (teday = f ( x ) ), ale je „zašumená“šumomz .Jemožnépoužiťy ako pomoc na získanie odhadu x,alenemôžemenutnevziaťinformáciuzy ako reprezentujúcu hodnotu,pretožeobsahujeajšum.

• stavová rovnica prechodu

x_k+1 = Ax_k + Bu_k + w_k

• rovnica výstupu

y_k = Hx_k + z_k

Keďže je pohyb hráča priamočiary,môžemepovedať,že stavpozostávaz jeho polohypa jeho rýchlostiv. Vstupná veličinau je nariadené zrýchlenie a výstupná veličinaje meraná poloha. Povedzme, že sme schopní meniť akceleráciu a merať polohu každých T _s sekúnd. V takomto prípade bude rýchlosť vdefinovaná rovnicou.

v_{k +1} = v_k + T_s u_k

To znamená, že rýchlosť vzdialená jednu vzorku od teraz (tedaTs sekúnd) bude rovná súčasnej rýchlosti prenásobenej nariadeným zrýchlením u a intervalomTs. Predošlá rovnica však nedáva presnú hodnotu preT _{k +1} . Namiesto toho bude rýchlosť ovplyvnená šumom. Šum rýchlosti je náhodnou premennou, ktorá sa mení s časom. Preto realistickejšie zapísaná rovnica vyzerá nasledovne:

v_{k +1}=v_k+T_s u_k + ~v_k

kde~v_kješum rýchlosti. Podobnú rovnicu je možne odvodiťajprepolohup:

p_k+1 = p_k + T_s v_k + T_s²u_k + ~p_k

kde~p_k je šum rýchlosti . Na základe čoho môžeme definovať stavový vektor, ktorý pozostáva z polohy a rýchlosti:

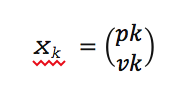
Keďže je meraná výstupná veličina úmerná polohe, je možné do rovníc za premenné A,B a H dosadiť nasledovné matice:

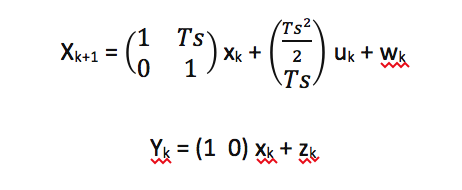
Kde matica A sa nazýva predikčná matica a matica B sa nazýva riadiaca matica. Keďže predpoveď nemusí byť sto percentne presná, vstupuje v tomto bode do procesu Kalmanov filter.Riešenie Kalmanovým filtrom nie je možné aplikovať kým nie sú splnené určité predpoklady o šume. Je potrebné si uvedomiť, že v rovniciach (modelu systému) v úvode vystupujú dve premenné -w je šum v procese az je šum v meraní. Taktiež je ďalej možné skonštatovať, že neexistuje korelácia medziw az - teda v akomkoľvek časek,w_kaz_k sú nezávislé náhodné premenné. Potom je možné zadefinovať kovariančné matice šumuQaRako:

• Kovariancia šumu v procese:

Q = (w_kw_k^T)

• Kovariancia šumu v meraní:

R = (z_kz_k^T)

kde w^T a z^T označujú transpozíciu náhodných vektorov šumov. Teraz je možné použiť Kalamnové rovnice.

Kalmanov filter sa delí na dve fázy. Predikčnú (časovú), vktorejsaurčujenový najlepší odhad ako predikcia z predchádzajúceho najlepšieho odhadu plus korekcia známych vonkajších vplyvov. A chyba kovariancie je predpovedaná na základe predchádzajúcej chyby kovariancie spolu s určitou dodatočnou chybou z prostredia.

Tieto hodnoty sú následne použité v druhej fáze Kalmanovho filtra, ktorá sa nazýva Korekčná (filtračná), ktorá pozostáva z rovníc na nájdenie , ktorý predstavuje odhad x v čase k (teda, to čo chceme nájsť). Druhý výraz v rovnici je tzv. Korekciaa reprezentuje veľkosť korekcie, akou treba korigovať odhad stavu na základe meraní.Rovnica K_ksa nazýva rovnica Kalmanovho zisku (zosilnenia). Rozborom rovnice pre K zistíme, že ak je šum z merania veľký,Rbude veľké, takže K bude malé a nebudeme dávať veľkú váhu meraniu y , keď budeme počítať ďalšie. Na druhej strane však ak je šum v meraní malý, R bude malé a K veľké, čo znamená, že meraniu priradíme veľkú váhu pri výpočte ďalšieho.